Что такое перекос фаз: Что такое перекос фаз, причины возникновения и возможность устранения?
Перекос фаз: как определить и что делать?
Чашка ароматного кофе, хрустящие тосты, чистая глаженая одежда – это лишь малая часть того, чтоб было бы невозможно, ну или очень сложно, не будь у нас электричества. Добавляя всё больше бытовых приборов для комфортной жизни, мы часто забываем о грамотном распределении нагрузок. И в результате начинаем замечать, что светильники стали тусклее, утюг греется дольше, барабан в стиральной машине или двигатель пылесоса раскручиваются с трудом, варочная панель не достигает максимальной температуры или не включается телевизор.
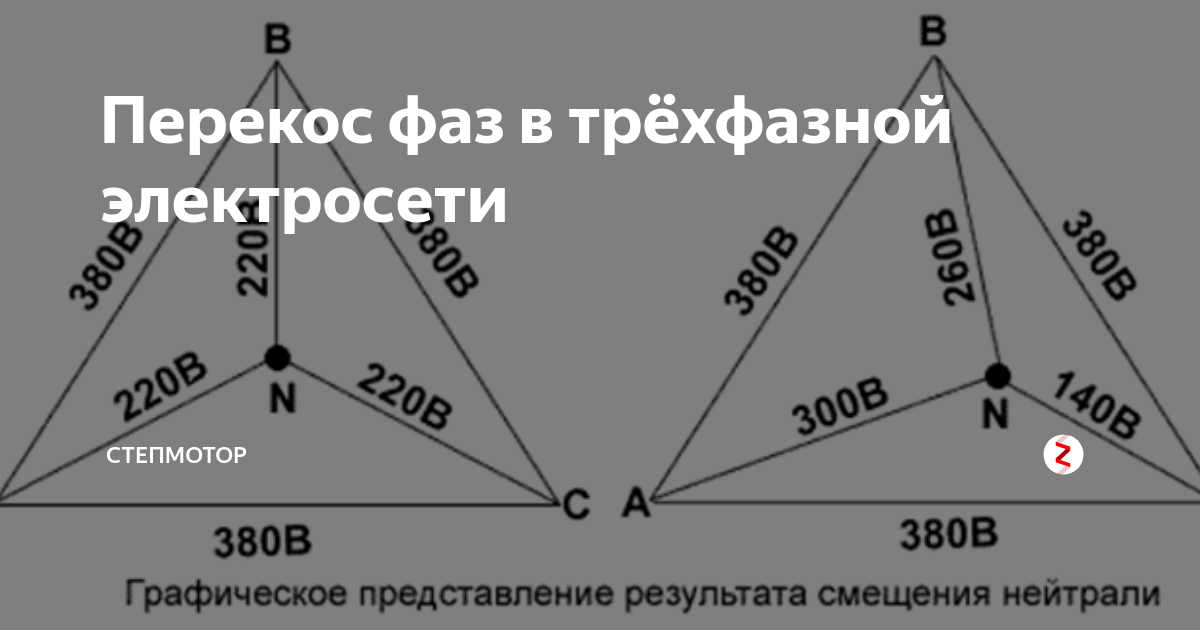
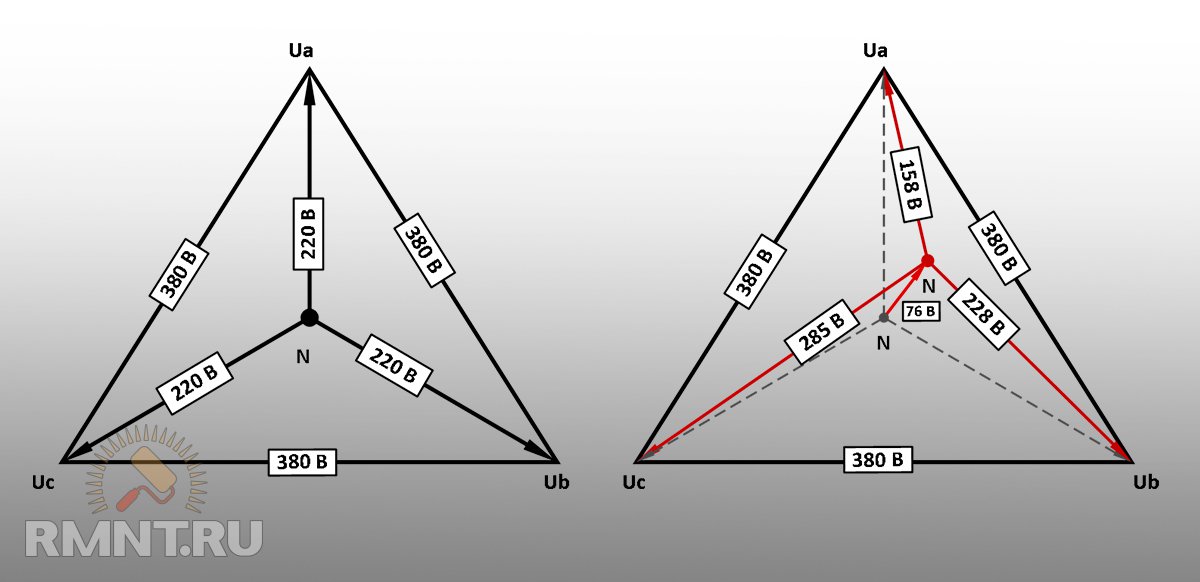
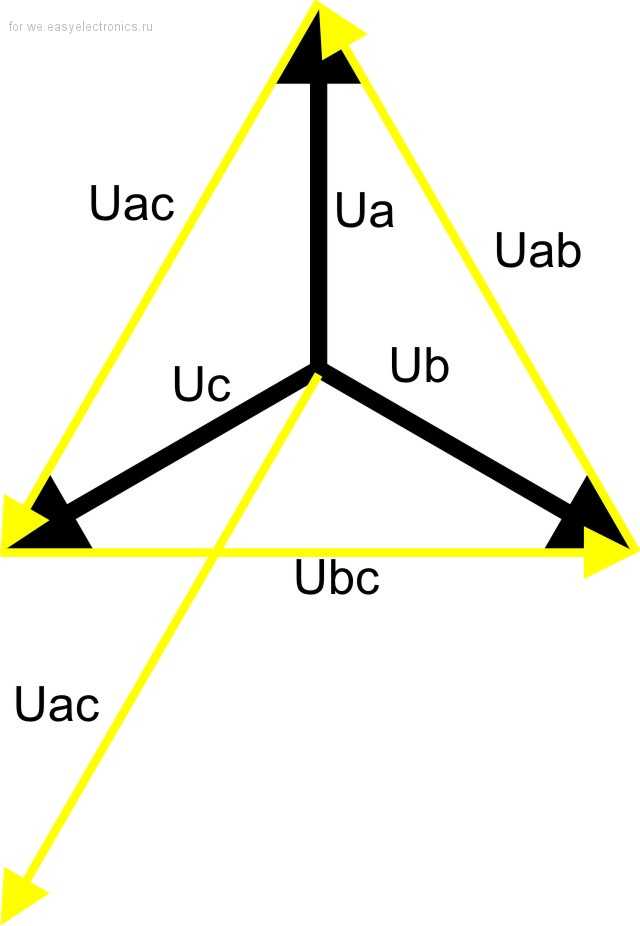
«Странное» поведение приборов говорит нам о том, что происходит перекос – явление, где на перегруженной фазе напряжение падает ниже нормы, тогда как на недогруженной происходит резкое повышение напряжения, превышающее пределы нормы. В трёхфазной сети такое явление могут вызвать три причины:
- Неверное распределение энергии между однофазными потребителями, которые включаются одновременно приводит перегрузке одной фазы и недогрузке второй.

- При обрыве, повреждении или дефекте нулевого провода, когда одна из оставшихся фазных жил берёт на себя функцию нейтрали, что создаёт резкое скачкообразное повышение напряжения.
- Заземление фазного провода может привести к срабатыванию УЗО или возникновению токов короткого замыкания.
Последствия любой из этих причин непредсказуемы, но всегда плачевны, а разница между ними кроется лишь в размере ущерба. Например, электроприбор может не выдержать скачок и сгореть, которое замыкание спроецирует электрический пожар, низкое напряжение, напротив, приведёт к недобору мощности и неэффективной работе техники. А при асимметрии фаз Вы будете приплачивать за электричество.
Стоит заметить, что «последствия легче предупредить…» Поэтому для защиты проводки и бытовой техники можно провести ряд профилактических мероприятий или добавить в цепь необходимое модульное электрооборудование.
Для однофазных цепей, которые всё ещё встречаются в старых домах или на дачах, перекос фаз гораздо опаснее, так как оборудование почти сразу даёт серьёзный сбой или сгорает. Чтобы обезопасить себя и продлить срок эксплуатации приборов, лучше включить в цепь следующие устройства:
Чтобы обезопасить себя и продлить срок эксплуатации приборов, лучше включить в цепь следующие устройства:
- Автоматические выключатели, которые при недопустимо высоком напряжении оперативно размыкают цепь в автоматическом режиме, предотвращая аварийные ситуации и поломку оборудования.
- Стабилизатор напряжения, который позволит предотвратить асимметрию в перераспределении нагрузок, и специальный трансформатор, который обеспечивает симметричное распределение нагрузок и обеспечивают стабильную работу однофазной сети. Последний вариант будет актуален для дач и частных домов.
- В редких случаях допускается применение конденсаторов с переменной ёмкостью и низкой токопроводимостью.
OptiDin BM63-1C32-УХЛ3 (6кА)
387,21
Выключатель автоматический MD63 1п 20 А 6 кА хар-ка C YON ДКС MD63-1C20-6
430,22
Выключатель автоматический 1п 32 А 4,5 кА хар-ка C Easy9 SE EZ9F34132
390,02
Выключатель автоматический ВА47-60 1п 32 А 6 кА хар-ка C KARAT ИЭК MVA41-1-032-C
292,40
Выключатель автоматический TX3 6000 1п 20 А 6 кА хар-ка C TX3 Legrand 403917
538,12
У трёхфазных цепей есть как минимум ещё две фазы «чтобы смягчить последствия».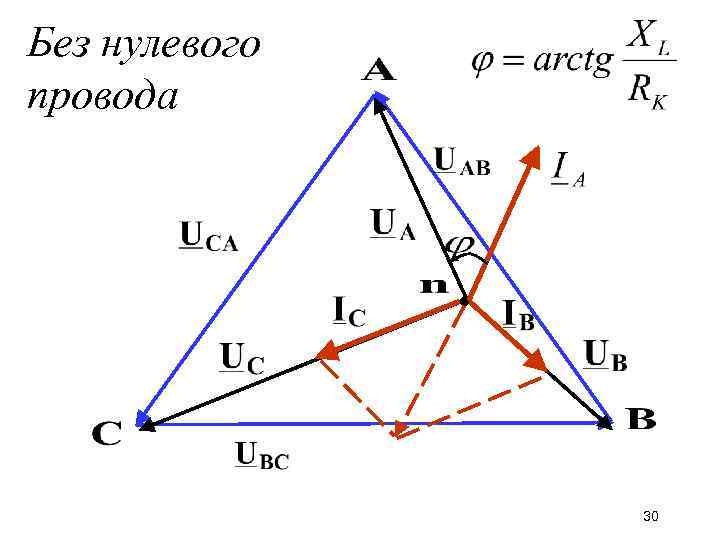
- Необходимо продумать заранее, а в случае проблем пересмотреть, существующую схему подключения электротехники, исходя из того, какие приборы будут работать одновременно.
- Включить в сеть трёхфазный стабилизатор, рассчитанный на предельно допустимую на заданном контуре нагрузку.
- Интегрировать в сеть реле контроля фазного тока, которое автоматически отслеживает уровень напряжения. И в случае резких скачков, которые превышают заданные допустимые значения, оперативно размыкает цепь и предотвращает аварийные ситуации.
- Установить трансформатор для симметричного распределения нагрузок и обеспечения бесперебойной работы сети независимо от количества и мощности подключённых потребителей.
Реле контроля фаз CZF-B DIN Евроавтоматика F&F EA04.001.002
1 650
1 291,35
Реле контроля фаз РК101-02 23301DEK
2 580
Реле контроля тока ORI 1,6-16А 24-240В AC/24В DC IEK ORI-01-16
1 882,37
Реле контроля напряжения 3-фазное РНПП-311 НОВАТЕК A8291-80108615
2 983
Перекос фаз — что такое, причины возникновения и устранение
Состояние всей техники в доме, офисе напрямую зависит не только от условий эксплуатации, обслуживания, но и от качества электроэнергии. Многие из нас даже не задумаются о том, что в этом вопросе важно соблюдать все стандарты, которые прописаны в соответствующей документации. Касается это, в том числе, и перекоса фазы.
Многие из нас даже не задумаются о том, что в этом вопросе важно соблюдать все стандарты, которые прописаны в соответствующей документации. Касается это, в том числе, и перекоса фазы.
Согласно ГОСТу этот показатель должен быть 4% по нулевой последовательности и 2% — по обратной.
Что значит перекос фаз?
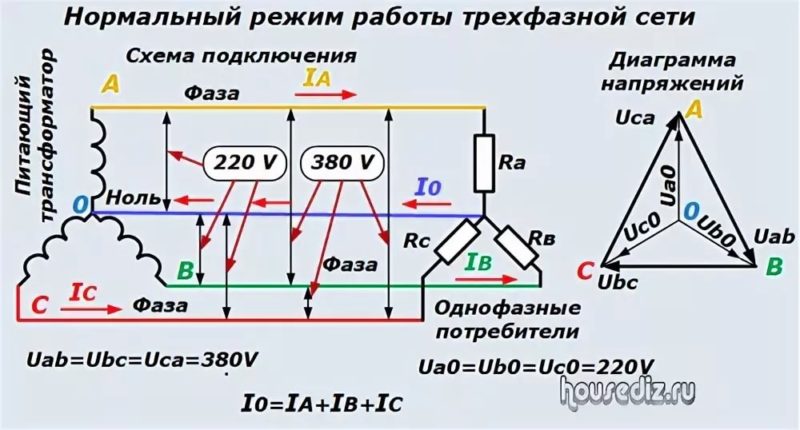
Этонесовпадение величин в трехфазных электросетях, вызванное неравномерным распределением нагрузки. Чаще всего возникает оно при раздаче напряжения устройствам однофазным. К примеру, это разводка сети на этаже по квартирам. Добиться паритета практически невозможно. С глухозаземленнойнейтралью в трехфазной сети выравнивает напряжение нейтраль. Именно она выполняет защитную роль, не допускает перекоса.
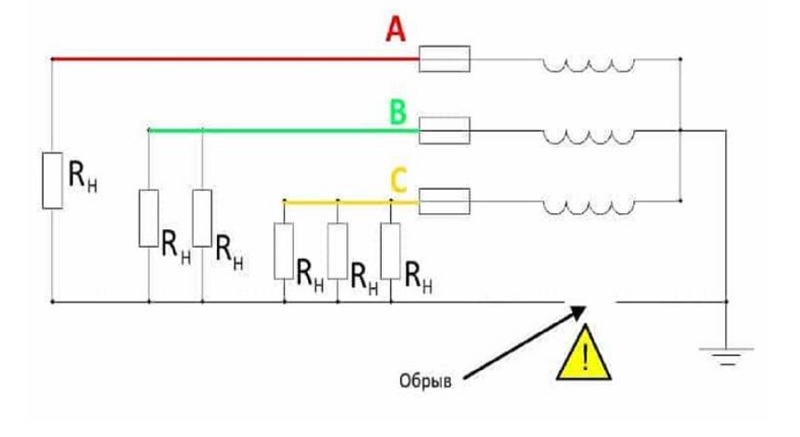
Меняют ситуацию и обрывы нуля. Тогда один из проводов фазы выполняет их функции, а величинаповрежденного нуля приближается к 380В.
Почему перекос фаз опасен?
Трехфазные устройства, способные работать с симметричными фазами, при перекосе вызывают нагрев обмотки, падение мощности. Это приводит не только к износу оборудования, но и иным неприятным и небезопасным ситуациям. Негативно сказываются перекосы и на источниках энергии:
Это приводит не только к износу оборудования, но и иным неприятным и небезопасным ситуациям. Негативно сказываются перекосы и на источниках энергии:
- Расход топлива существенно увеличивается, что влечет дополнительные затраты.
- Генератор испытывает огромную нагрузку, которая уменьшает срок службы устройства.
- При работе на пределе велик риск серьезных поломок.
Стоит упомянуть и о том, что это несет угрозу человеку. К примеру, это может спровоцировать поражение токов, вывести из строя бытовые устройства и прочее.
Можно ли избежать перекоса фаз?
Безусловно, об этом стоит позаботиться еще при проектировании электросети. Важно правильно распределить нагрузку между фазами, а также учесть ее изменение при эксплуатации. Устранить перекосы позволяет и частотный преобразователь Данфос, использование стабилизаторов.
Спасти ситуацию может и защитная автоматика. К ней относится реле контроля. При аварийной ситуации оно отключает цепь, тем самым предотвращая трагедию.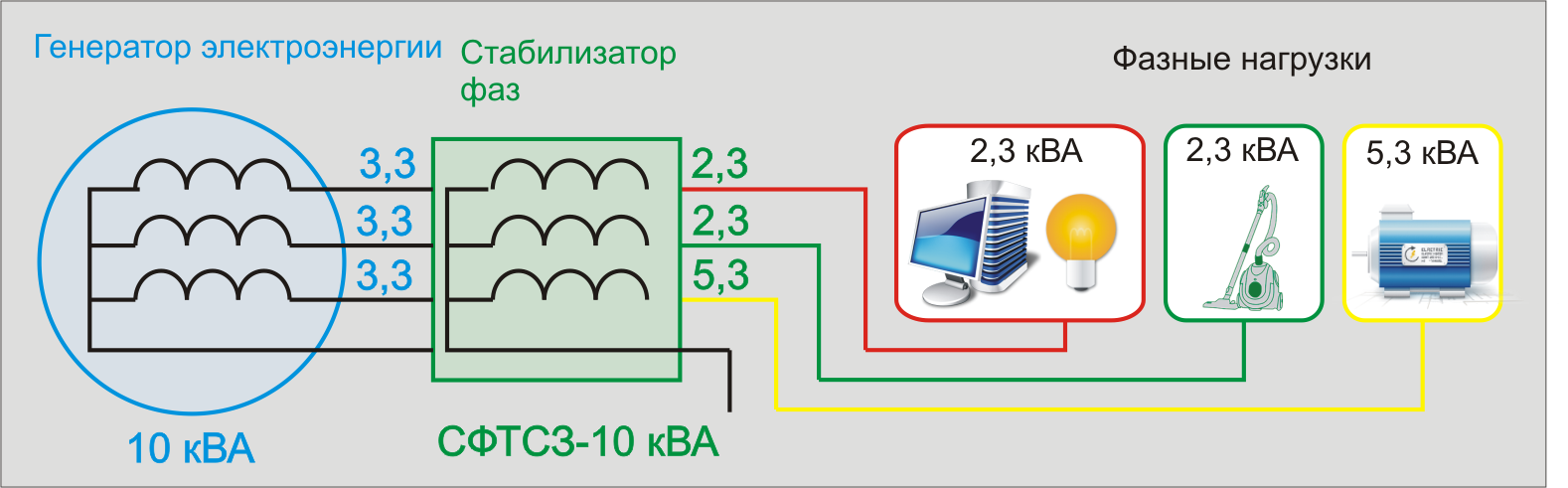
Однофазные сети защитить от аварий можно с помощью реле напряжения. Оно отключает питание, если напряжение выходит за определенные пределы. Установка защитного оборудования позволит избежать больших финансовых потерь и при этом обеспечить безопасность.
Заключение
Перекос фаз довольно опасен, поэтому не стоит экономить на оборудовании. Правильнее установить защитные устройства и доверять обслуживание электросетей специалистами.Так вы не только будете уверены в своей безопасности, но и сэкономите средства на технике. Подобрать реле или приобрести частотный преобразователь Данфос вы можете у нас. Мы предлагаем качественное и надежное оборудование. Все изделия сертифицированы. Кроме того, наши специалисты проконсультируют вас по любому вопросу, в том числе и выбора.
Формула фазового сдвига — Изучите формулу для расчета фазового сдвига
Формула фазового сдвига используется для нахождения фазового сдвига функции. Фазовый сдвиг — это сдвиг, когда график функции синуса и косинуса смещается влево или вправо от их обычного положения, или можно сказать, что при фазовом сдвиге функция сдвигается по горизонтали, насколько далеко от обычного положения. Как правило, функции смещены (π/2) от обычного положения. Давайте узнаем больше о формуле фазового сдвига вместе с решенными примерами в следующем разделе.
Как правило, функции смещены (π/2) от обычного положения. Давайте узнаем больше о формуле фазового сдвига вместе с решенными примерами в следующем разделе.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронируйте бесплатный пробный урок
Формула фазового сдвига для синусоидальной кривой показана ниже, где выражены как горизонтальные, так и вертикальные сдвиги. Фазовый сдвиг может быть как положительным, так и отрицательным в зависимости от направления сдвига от начала координат. Формула фазового сдвига может быть выражена как
у = A sin(B(x + C)) + D
также F(x) = Asin(Bx − C)+D.
, где
- (C/B) представляет фазовый сдвиг.
- А – амплитуда.
- Пример 1: Выясните, каков фазовый сдвиг синуса, имеющего F(t)= 3 sin(4(x − 0,5)) + 2, используя формулу фазового сдвига.

Решение:
Чтобы найти: фазовый сдвиг синусоидального сигнала
Используя формулу фазового сдвига,
y = A sin(B(x + C)) + D
Сравнивая данное уравнение с формулой фазового сдвига
Получаем
Амплитуда, A = 3 π/2
Вертикальный сдвиг, D = 2
Таким образом, фазовый сдвиг будет равен −0,5
, что соответствует сдвигу вправо на 0,5.
Ответ: Фазовый сдвиг данной синусоидальной функции на 0,5 вправо.
- Пример 2: Найдите фазовый сдвиг F(t)=3sin(4t+3) с помощью формулы фазового сдвига.
Найти: Разность фаз синусоиды
Дано:
Амплитуда, A = 3
Период, 2π/B = 2π/4 = π/2
Вертикальный сдвиг, D 0
Используя формулу фазового сдвига,
F(x) = Asin(Bx−C) + D.

C/B представляет фазовый сдвиг
Фазовый сдвиг = -3/4
Ответ: Фазовый сдвиг данной синусоидальной функции равен -3/4.
Перейти к Slidego, чтобы скользить
Математические листы и
Визуальная учебная программа
Калькулятор фазового сдвига
, созданный Maciej Kowalski, PhD Candidate
, обзор Anna Szczepanek, PhD и Steven Wording
Last Advated: 202222222222222222222222222222222222222222222222222222222222222222222222222222292222н Содержание:
- Амплитуда, период, фазовый и вертикальный сдвиг
- Как найти амплитуду
- Как найти период
- Как найти фазовый сдвиг
- Как найти вертикальный сдвиг
- Пример: с помощью калькулятора амплитудно-периодного фазового сдвига мы изучим тригонометрические функции и как вычислить их фазовый сдвиг. На самом деле мы рассмотрим больше: мы также объясним, как найти амплитуду и как найти период .
 На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.
На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.Амплитуда, период, фазовый сдвиг и сдвиг по вертикали
Как мы упоминали выше, здесь мы сосредоточимся на тригонометрических функциях , точнее на синусе и косинусе. Тем не менее, важно помнить, что многие понятия являются более общими , особенно понятия горизонтального переноса или вертикального сдвига.
Прежде всего, давайте посмотрим на картинку, показывающую , где амплитуда, период, фазовый сдвиг и вертикальный сдвиг отображаются на графике (обратите внимание, что такое же изображение появляется в верхней части калькулятора фазового сдвига Omni).
Мы можем записать такие функции с помощью формулы (иногда называемой уравнением фазового сдвига или формулой фазового сдвига ):
f(x)=A⋅sin(Bx−C)+D,f(x ) = A\cdot\sin(Bx-C)+D,f(x)=A⋅sin(Bx−C)+D,
или:
f(x)=A⋅cos(Bx−C )+D,f(x) = A\cdot\cos(Bx-C)+D,f(x)=A⋅cos(Bx−C)+D,
, где AAA, BBB, CCC, DDD произвольные действительные числа, но с ненулевыми AAA и BBB (иначе это не была бы тригонометрическая функция).

Амплитуда показывает, насколько далеко (в любом направлении) отходят значения от центральной линии графика. Для простого синуса или косинуса его значение равно 111, так как центральная линия находится в точке 000, а значения функции находятся в диапазоне от -1-1-1 до 111.
Период — это длина по горизонтальной оси, после которой функция начинает повторяться. Другими словами, (бесконечный) граф — это всего лишь набор копий длины периода, склеенных вместе на концах . Для простого синуса или косинуса период равен 2π2\pi2π, поскольку sin(0)=sin(2π)=sin(4π)=…\sin(0) = \sin(2\pi) = \ sin(4\pi) = …sin(0)=sin(2π)=sin(4π)=… и части между ними точно такие же (и аналогично для косинуса).

Фазовый сдвиг (также называемый горизонтальным сдвигом или горизонтальным сдвигом ) описывает, насколько по горизонтали график сместился от обычного синуса или косинуса. Таким образом, значение равно 000, если две функции не изменены.
Вертикальный сдвиг (также называемый вертикальным сдвигом ) описывает, насколько вертикально график сместился от обычного синуса или косинуса. Другими словами, это близнец фазового сдвига, который касается перпендикулярное направление . В частности, значение снова равно 000, если обе функции остаются неизменными.
Итак, мы узнали, что такое фазовый сдвиг, а также три сопутствующих значения. Разделы ниже описывают , как вычислить каждый из них на основе обозначений из приведенной выше формулы фазового сдвига. Сначала мы покажем , как найти амплитуду .

Введенное нами понятие широко распространено при изучении колебательных и гармонических движений. Короче говоря, эти явления — лучшие друзья тригонометрии. Вы можете обнаружить связь на нашем калькуляторе тригонометрии или узнать больше о различных функциях, которые постоянно появляются, когда вы анализируете маятник, на калькуляторе тригонометрических функций или на более конкретном калькуляторе косинуса и калькуляторе синуса!
Как найти амплитуду
Мы знаем, что функции синуса и косинуса имеют значения в диапазоне от −1-1−1 до 111. Более того, этот простой факт не меняет , если мы подставим sin(x )\sin(x)sin(x) или cos(x)\cos(x)cos(x) для sin(Bx−C)\sin(Bx — C)sin(Bx−C) или cos( Bx−C)\cos(Bx — C)cos(Bx−C) для ненулевого BBB и произвольного CCC. На самом деле, это потому, что функция f(x)=Bx−Cf(x) = Bx – Cf(x)=Bx−C является тогда биекцией (т. е. взаимно-однозначным соответствием) на пространство вещественные числа.
Теперь давайте посмотрим, что произойдет, если мы добавим DDD, то есть если у нас есть sin(Bx−C)+D\sin(Bx — C) + Dsin(Bx−C)+D или cos(Bx−C) +D\cos(Bx — C) + Dcos(Bx−C)+D вместо этого.
 Поскольку первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что осевая линия приходится на DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.
Поскольку первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что осевая линия приходится на DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.Следовательно, единственное, что может повлиять на амплитуду в формулах фазового сдвига A⋅sin(Bx−C)+DA\cdot\sin(Bx — C) + DA⋅sin(Bx−C)+D и A⋅cos (Bx−C)+DA\cdot\cos(Bx — C) + DA⋅cos(Bx−C)+D — это ненулевое AAA. И действительно, поскольку sin(Bx−C)\sin(Bx-C)sin(Bx−C) и cos(Bx−C)\cos(Bx-C)cos(Bx−C) все это время находятся между −1-1−1 и 111, множитель AAA изменяет этот диапазон на −1⋅A=−A-1\cdot A = -A−1⋅A=−A и 1⋅A=A1 \cdot A = A1⋅ А=А.
Да, вы уже догадались: амплитуда уравнений фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx — C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C)+DA \cdot\cos (Bx — C) + DA⋅cos(Bx−C)+D просто равно AAA.

Как найти период
Напомним, что функции синуса и косинуса имеют периоды, равные 2π2\pi2π, т. е. имеем sin(x+2π)=sin(x)\sin(x + 2\ pi) = \sin(x)sin(x+2π)=sin(x) и cos(x+2π)=cos(x)cos(x + 2\pi) = cos(x)cos(x+2π) =cos(x) для любого xxx. В частности, это дает: !\sin(x\!+\!2\pi)\!+\!D\!=\!A\!\cdot\!\sin(x)\!+\!D,A⋅sin(x+ 2π)+D=A⋅sin(x)+D,
и:
A ⋅ cos(x + 2π) + D = A ⋅ cos(x) cdoll+\s (x\!+\!2\pi)\!+\!D\!=\!A\!\cdot\!\cos(x)\!+\!DA⋅cos(x+2π)+D= A⋅cos(x)+D
Итак, мы видим, что AAA и DDD в формуле фазового сдвига не влияют на период . Действительно, все сводится к тому, что происходит внутри тригонометрических функций . И еще:
sin(x−C+2π)=sin(x−C),\sin(x — C + 2\pi) = \sin(x — C),sin(x−C+2π )=sin(x−C),
и:
cos(x−C+2π)=cos(x−C)\cos(x — C + 2\pi) = \cos(x — C)cos(x−C+2π)=cos(x− C)
По тем же правилам, что и выше, поэтому это не CCC или , которые выполняют эту работу.
 Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.Мы снова обратимся к комментарию, который мы начали с , чтобы понять, почему и как BBB влияет на периодичность в уравнениях фазового сдвига A⋅sin(Bx−C)+DA \cdot \sin(Bx — C) + DA⋅sin (Bx−C)+D и A⋅cos(Bx−C)+DA \cdot \cos(Bx — C) + DA⋅cos(Bx−C)+D. Ведь:
грех(Bx)=sin(Bx+2π)=sin(B ⋅ (x+2πB) )\begin{split} \sin(Bx) &= \sin(Bx + 2\pi)\\[.8em] & = \sin\left(B\! \cdot\! \left(x + \frac{2\pi}{B}\right)\!\right) \end{split}sin(Bx)=sin(Bx+2π)=sin(B⋅(x+B2π))
Таким образом, с добавлением каждых 2π/B2\pi/B2π/B к аргументу xxx, мы возвращаемся в то же место , и функция повторяется (аналогично для косинуса).
Всего период уравнения фазового сдвига равен 2π/B2\pi/B2π/B.
Наши ежедневные знания о волнах обычно отдают предпочтение частоте за период; однако это почти одно и то же. Узнайте почему на частотном калькуляторе Omni.

Как найти фазовый сдвиг
По определению фазовый сдвиг описывает горизонтальный сдвиг функции относительно обычного sin(x)\sin(x)sin(x) или cos(x) \ соз (х) соз (х). Таким образом, у основных функций он равен 000. Фактически, если мы сравним их графики:
…мы заметим, что мы можем получить одним переводом другого (на самом деле взаимные кофункции имеют много общего). Точнее, имеем следующее:
sin(x+π2)=cos(x),\sin\left(x+\frac{\pi}{2}\right)=\cos(x), sin(x+2π)=cos(x),
и:
cos(x−π2)=sin(x)\cos\left(x-\frac{\pi}{2}\right )=\sin(x) cos(x−2π)=sin(x)
В приведенном выше примере уже показано, где в A⋅sin(Bx−C)+DA \cdot\sin(Bx — C) + DA ⋅sin(Bx−C)+D и A⋅cos(Bx−C)+DA \cdot\cos(Bx — C) + DA⋅cos(Bx−C)+D следует искать значения, отвечающие за фазовые сдвиги. Однако, в отличие от амплитуды и периода, на этот раз нам понадобятся две из четырех букв .
В общем случае (то есть не только в уравнениях фазового сдвига) мы получаем горизонтальный сдвиг произвольной функции f(x)f(x)f(x) вычислением f(x−a)f( x — a)f(x−a): сдвиг графика на aaa вправо.
 Другими словами, мы заменяем каждое вхождение xxx на x−ax — ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x — a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:
Другими словами, мы заменяем каждое вхождение xxx на x−ax — ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x — a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:потому что(3(x−a)+1)=cos(3x−3a+1)\begin{split} \cos&(3(х-а)+1)\\ &=\cos(3x-3a+1) \end{split}cos(3(x−a)+1)=cos(3x−3a+1)
Другими словами, нельзя забывать о множителях, стоящих перед xxx.
В нашем случае формула фазового сдвига дает:
A⋅sin(Bx−C)+D=A⋅sin(B⋅(x−CB))+D,\begin{split} A\cdot&\sin(Bx-C)+D\\ =A\cdot&\sin\left(B\cdot\left(x-\frac{C}{B}\right)\right)+D, \end{split}A⋅=A⋅sin(Bx−C)+Dsin(B⋅(x−BC))+D,
, что равно фазовый сдвиг на C/BC/BC/B (вправо) функции A⋅sin(Bx)A \cdot\sin(Bx)A⋅sin(Bx). Конечно, мы можем повторить вышеописанное и для косинуса.
Подводя итог, чтобы вычислить фазовый сдвиг уравнения фазового сдвига, нужно найти C/BC/BC/B.

Как найти вертикальный сдвиг
Это легко , особенно теперь, когда мы узнали, что такое фазовый сдвиг, амплитуда и период и как их вычислить. Давайте опираться на то, что мы уже узнали.
Мы знаем, что в формулах фазового сдвига A⋅sin(Bx−C)+DA \cdot\sin(Bx — C) + DA⋅sin(Bx−C)+D и A⋅cos(Bx−C )+DA \cdot\cos(Bx — C) + DA⋅cos(Bx−C)+D, AAA определяет, насколько сильно колеблются значения по обе стороны от центральной линии. BBB указывает, насколько далеко мы расширяем выпуклости графика и, как результат, как быстро мы можем повторять значения. Кроме того, вместе с CCC они описывают, сдвинули ли мы функцию влево или вправо и насколько.
Очевидно, горизонтальное смещение не влияет на вертикальное смещение : в конце концов, это два перпендикулярных направления. С другой стороны, амплитуда только говорит нам, как далеко по вертикали простирается график, но не сдвигает его . В общем, у нас осталась только одна буква : DDD.

DDD в уравнениях фазового сдвига точно соответствует вертикальному сдвигу . Он определяет диапазон функции, т. е. насколько далеко от обычной версии без DDD мы сдвигаем график.
На этом теоретическая часть на сегодня завершена. пора посмотреть как рассчитать фазовый сдвиг на красивом примере . И знаешь, что? Мы также покажем, как найти период, амплитуду и сдвиг по вертикали. В конце концов, почему бы и нет? Больше математических расчетов = больше удовольствия!
Пример: использование калькулятора фазового сдвига амплитуды периода
Давайте посмотрим как найти амплитуду, период, фазовый сдвиг и вертикальный сдвиг функции f(x)=0,5⋅sin(2x−3)+ 4f(x) = 0,5 \cdot\sin(2x — 3) + 4f(x)=0,5⋅sin(2x−3)+4. Во-первых, мы позволим калькулятору фазового сдвига Omni говорить за вас.
В верхней части нашего инструмента нам нужно выбрать функцию, которая появляется в нашей формуле.
 В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx — C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее:
В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx — C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее:A=0.5B=2C=3D=4\begin{split} А&=0,5\\ В&=2\\ С&=3\\ Д&=4 \end{split}ABCD=0.5=2=3=4
(Обратите внимание, что еще до того, как мы введем значения, калькулятор фазового сдвига отображает график функции sin(x)\sin(x)sin(x). Это потому, что инструмент понимает , не дающее определенных значений, как отсутствие числа в соответствующих местах в формуле . Таким образом, он вообще не считывает ввод как A = 1A = 1A = 1, B = 1B = 1B = 1, C = 0C = 0C = 0 и D = 0D = 0D =0, что дает:
1⋅sin(1⋅x−0)+0=sin(x)1 \cdot \sin(1\cdot x — 0) + 0 = \sin(x)1⋅ sin(1⋅x−0)+0=sin(x)
Момент, когда мы даем последнее значение, график функции появляется под вместе с амплитудой, периодом, фазовым сдвигом и вертикальным сдвигом ниже.
 Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.
Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.Теперь объясним как самим найти фазовый сдвиг и все остальные значения . Для этого достаточно вспомнить четыре раздела выше, чтобы вычислить, что:
- Амплитуда : А=0,5А = 0,5А=0,5;
- Период равен 2π/B=2π/2=π2\pi / B = 2\pi / 2 = \pi2π/B=2π/2=π;
- Фазовый сдвиг равен C/B=3/2=1,5C / B = 3/2 = 1,5C/B=3/2=1,5; и
- Вертикальное смещение равно D=4D = 4D=4.
В общем, график выглядит так :
Пара пустяков, не так ли? Не забудьте поиграться с калькулятором фазового сдвига, чтобы увидеть , как различные коэффициенты влияют на график . А когда вам это наскучит, переходите к другим тригонометрическим калькуляторам Omni и приготовьтесь получить еще больше удовольствия от !
Часто задаваемые вопросы
Как рассчитать фазовый сдвиг?
Чтобы вычислить фазовый сдвиг функции вида
A × sin(Bx - C) + DилиA × cos(Bx - C) + D, необходимо:- Определить
Б.
- Определить
C. - Разделить
К/Б. - Помните , что если результат:
- Положительный , график сдвинут вправо.
- Отрицательный , график смещен влево.
- Наслаждайтесь игрой , обнаружив фазовый сдвиг.
Как найти фазовый сдвиг по графику?
Чтобы найти фазовый сдвиг по графику , необходимо:
- Определить , является ли сдвинутым синусоидальным или косинусным.
- Посмотрите на график справа от вертикальной оси.
- Найдите первый:
- Пик , если коэффициент перед функцией положительный; или
- Корыто , если коэффициент отрицательный.
- Рассчитать расстояние от вертикальной линии до этой точки.

- Если функция была синусоидальной, вычесть
π/2из этого расстояния. - Наслаждайтесь найдя фазовый сдвиг по графику.
Как найти амплитуду, период и фазовый сдвиг?
Нахождение амплитуды, периода и фазового сдвига функции вида
A × sin(Bx - C) + DилиA × cos(Bx - C) + Dвыполняется следующим образом:- Амплитуда равна
A; - Период равен
2π / B; и - Фазовый сдвиг равно
C/B.
Как графически отображать триггерные функции с фазовым сдвигом?
Для графических триггерных функций с фазовым сдвигом необходимо:
- Определить , что такое триггерная функция.
- Фокус на точку
(0,0)на плоскости. - Если фазовый сдвиг:
- Положительный , двигаться вправо.

- Положительный , двигаться вправо.



 На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.
На деле оказывается, что огромный класс функций ведет себя практически одинаково, а различия сводятся к описанию тех самых значений, о которых говорилось выше; амплитуда, период и фазовый сдвиг. ну до вертикальное смещение , по крайней мере.


 Поскольку первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что осевая линия приходится на DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.
Поскольку первая часть дает что-то между -1-1-1 и 111, все это будет между -1+D-1 + D-1+D и 1+D1 + D1+D (см. Как найти вертикальную сдвиг для сравнения). Это означает, что осевая линия приходится на DDD, а амплитуда по-прежнему равна 111, потому что значения отклоняются на 111 от DDD.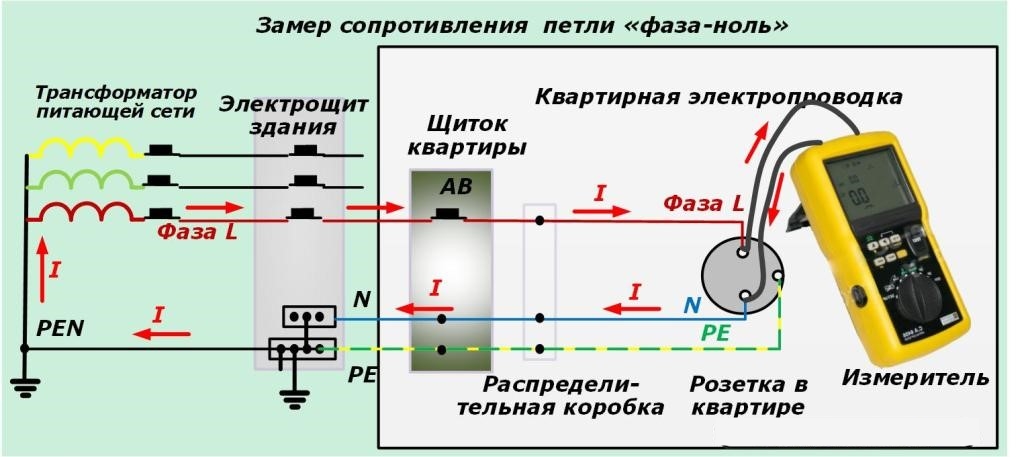
 Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
Таким образом, с отброшенными тремя вариантами должен быть четвертый : BBB.
 Другими словами, мы заменяем каждое вхождение xxx на x−ax — ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x — a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:
Другими словами, мы заменяем каждое вхождение xxx на x−ax — ax−a в формуле для f(x)f(x)f(x). Например, применение преобразования к sin(x)\sin(x)sin(x) дает sin(x−a)\sin(x — a)sin(x−a), но, скажем, для cos (3x+1)\cos(3x + 1)cos(3x+1) мы получим:
 В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx — C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее:
В нашем случае мы выбираем « синус » под « Тригонометрическая функция в f ». Это вызовет символическое представление такого уравнения фазового сдвига : f(x)=A⋅sin(Bx−C)+Df(x) = A \cdot\sin(Bx — C) + Df(x )=A⋅sin(Bx−C)+D. Оглядываясь на то, что у нас есть, мы вводим следующее: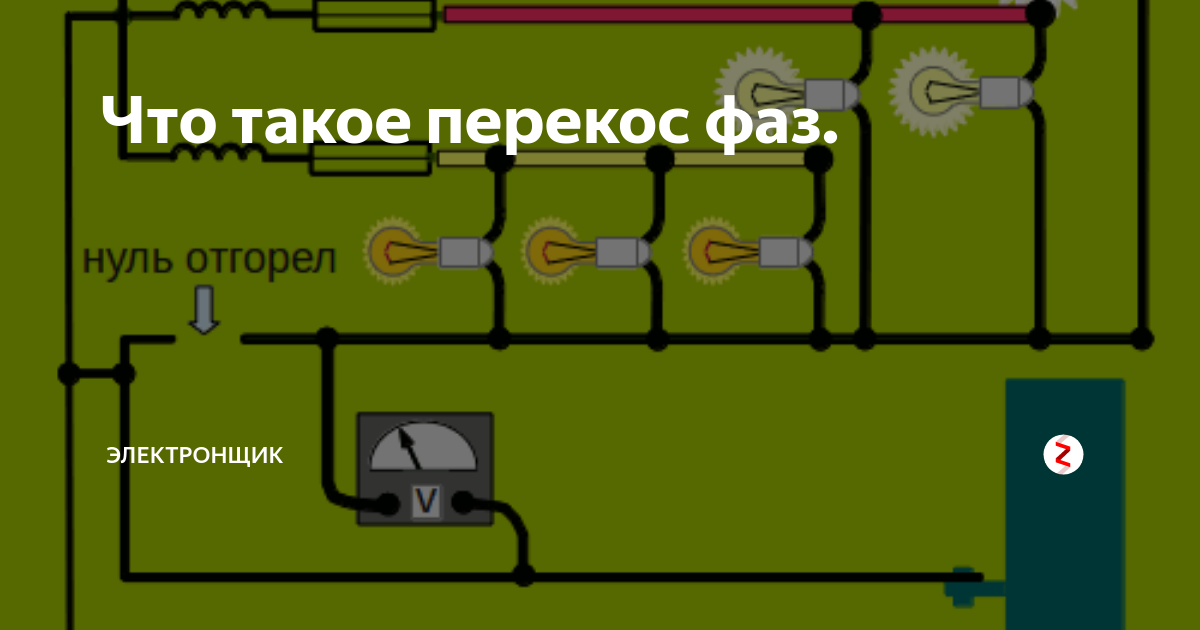 Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.
Также обратите внимание, что при необходимости вы можете перейти в расширенный режим калькулятора, чтобы найти значение функции в любой точке x0x_0x0.

Добавить комментарий