Как называется кривая линейка: Ответы на кроссворды и сканворды онлайн
«Кривая» линейка, 6 букв, сканворд
Подошло Не подошло
«Кривая» линейка
Альтернативные описания
• инструмент портного и чертежника
• инструмент, который применяют при черчении, когда циркуль не помогает
• фигурная линейка для вычерчивания кривых линий
• чертежный инструмент для вычерчивания кривых линий
• чертежный инструмент, фигурная линейка
• шаблон, модель, применяемые при изготовлении изделий сложного профиля
• фигурная линейка
• «криволинейка»
• какую линейку можно получить, если у известного шоумена поменять первую букву?
• линейка для того, кто предпочитает окольные пути
• фигуристая линейка
• линейка закройщика
• инструмент для разметки
• линейка-кривляка
• шаблон для обводки
• шаблон, линейка
• изогнутая линейка
• «кривая» линейка
• линейка модельера
• шаблон для обводов
• кривая линейка портного
• линейка с загогулинами
• инструмент для разведки
• линейка для выкроек одежды
• чертежный инструмент
• «кривляка» среди линеек
• чертежная линейка
• линейка с изгибами
• загогулистая линейка
• линейка с выкрутасами
• линейка
• линейка-шаблон с выкрутасами
• линейка «ищущих окольные пути»
• фигурный шаблон
• «портнографическая» линейка
• швейная «линейка»
• рифма к Цекало
• кривой трафарет чертежника
• «вертлявая» линейка закройщика
• линейкакривляка
• криволинейный шаблон портного
• фигурная линейка портного
• линейка для кривых линий
• линейка «любителя окольных путей»
• шаблон
• неровная линейка
• хитроумная линейка
• «букет кривых»
• линейка обтекаемых форм
• шаблонная линейка
• Инструмент для вычерчивания кривых линий
• Чертежный инструмент для проведения или проверки кривых линий
• Измерительный инструмент, шаблон
• Фигуристая линейка
• «Букет кривых»
• «Вертлявая» линейка закройщика
• «Кривляка» среди линеек
• «Криволинейка»
• «Линейка» закройщика
• «Портнографическая» линейка
• какую линейку можно получить, если у известного шоумена поменять первую букву
• линейка «ищущих окольные пути»
• линейка «любителя окольных путей»
• линейка-шаблон
• ср.
выкройка, образец для внешних очерков вещи; кривые правила разного вида, для криволинейных чертежей, особенно корабельных; вытесанный из досок по чертежу, в полную величину, образец, для обделки по нем корабельных членов и железных скреплений; вырезка по чертежу в дощечке, для обделки литейных болванов, для тяги штукатурных карнизов; снаряд для калиброванья, измеренья ядер. Пск. твер. бот или ботало, двухсаженная мутовка рыбаков, для сгону рыбы; вероятно от лакать, пугать; арх. деревянные путы на оленя, колодка на ногу; вероятно, от лекан м. перм. отрубок, чурбашек. Лекальный, к лекалу относящ. Лекальщик м. обделывающий лекала. Лекальная ж. мастерская, где изготовляют и пригоняют лекала по чертежам. Лекать пск. твер. вернее лякать малорос. пугать, загонять рыбу лекалом, рыбачить при помощи его, ботать
• швейная «линейка»
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кривая линейка Яндекс.Карт
Это экватор.
Кривая линейка Яндекс.Кар
Блин. Затупил немного — нет, все локсодромии прямые только на Меркаторе. Всё. То есть должны быть и цилиндричность, и равноугольность. Wiki it!
Просто глобус, который можно приближать-удалять. Там, я так понимаю, вообще искажений нет. Это ж глобус.
48184250%2C5.20218746~130.07797405%2C23.02019655
(В смысле точек бесконечно много поставить)Изогнутые линии – значение, примеры, типы и часто задаваемые вопросы
Изогнутая линия определяется как линия, которая не прямая, а изогнутая. В идеале прямая линия имеет нулевую кривизну, тогда как изогнутая линия имеет ненулевую кривизну и является непрерывной и гладкой. Кривые — это выдающиеся фигуры, встречающиеся повсюду вокруг нас. Вы можете заметить изгибы в искусстве, украшении или вообще предмете, а кривые — это фигуры, которые можно увидеть повсюду вокруг вас. Первоначально линии могли быть изогнутыми или прямыми. В сегодняшнем математическом использовании, для точного различия, кривая — это что-то изогнутое, а линия — это что-то прямое.
Кривые линии часто используются для графического представления функций, поскольку это одна из важнейших тем в области математики.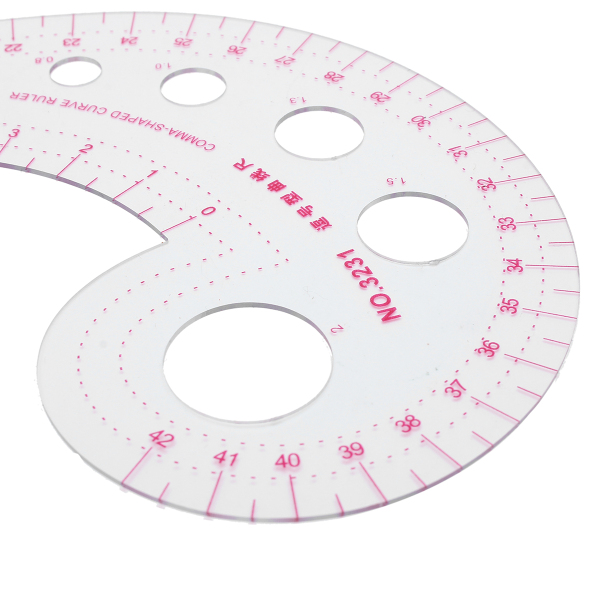
Дифференциация между кричащими линиями и прямыми линиями
Кричная линия | Прямая линия |
A Сглапная линия Bent Bent Bent Bent Bent Bent Bent. | Кратчайшая линия, соединяющая любые две точки, называется прямой линией. |
Точки, определяющие кривую, меняют направление от одной точки к другой. | Прямая линия представляет собой последовательность нескольких точек, выровненных в одном направлении. |
Кривая линия всегда имеет ненулевую кривизну, которая может быть положительной или отрицательной. | Прямая линия всегда имеет нулевую кривизну. |
Изогнутые линии не двигаются в одном направлении. Направление постоянно меняется от одной точки к другой. | Прямые линии движутся в одном направлении. |
Примеры изогнутых линий
Существует множество примеров изогнутых линий. Наиболее распространенным и ярким примером изогнутых линий являются буквы алфавита C и S. Эти буквы алфавита изогнуты. Напротив, другие буквы, такие как L, N, A, Z и другие, являются подходящими примерами прямых линий, поскольку они не являются кривыми, а являются соединенными сегментами двух или более последовательных линий.
Типы изогнутых линий
Существует множество различных типов изогнутых линий. Тем не менее, есть несколько известных типов изогнутых линий:
1. Открытая кривая
Изогнутая линия или кривая называется открытой, если ее конечные точки не пересекаются. В открытой изогнутой линии конечные точки никогда не встречаются.
Парабола — прекрасный пример незамкнутой кривой.
2. Замкнутая кривая
Кривая называется замкнутой, если ее начальная точка совпадает с конечной.
Круг или затмение — прекрасный пример замкнутой кривой.
3. Простая кривая
Простая кривая не пересекает сама себя. Некоторые кривые самопересекающиеся; однако простая кривая не пересекается сама с собой.
4. Алгебраическая кривая
Алгебраическая кривая представляет собой плоскую кривую, в которой множество точек размещено на евклидовой плоскости и представлено в виде многочленов. Степень кривой обозначается степенью многочлена.
Например, C = {(a, b) ∈ R2: P(a, b) = 0}
5. Трансцендентальная кривая
изгиб. Трансцендентная кривая состоит из бесконечного числа точек перегиба и множества точек пересечения, которые будут прямыми.
Это не многочлен в точках a и b.
6. Кривая изокванты
Термин «изокванта» представляет собой объединение двух терминов: «изо» означает «равно», а слово «количество» относится к количеству. Таким образом, термин изокванта определяется как кривая выпуклой формы, образованная соединением точек. Кривая изокванты помогает организациям и предприятиям регулировать затраты, чтобы максимизировать производство и прибыль.
Изогнутая линия
«Кривая линия» или просто «Кривая» — это непрямая линия. Кривые можно найти повсюду вокруг нас. Кривые можно найти повсюду вокруг нас, будь то искусство, декор или повседневная жизнь. В этом посте мы изучим концепцию изогнутой линии, а также различные типы изогнутых линий и несколько экземпляров.
Что такое кривая линия?
Изогнутая линия — это изогнутая, а не прямая линия. В идеальной ситуации он должен быть плавным и непрерывным.
Другими словами, кривая — это набор точек, которые напоминают прямую линию и попадают между двумя точками. Кривизна прямой линии, как известно, равна нулю. В результате мы можем назвать линию изогнутой, если ее кривизна больше нуля. Различные виды изогнутых линий изображены на диаграмме ниже.
(Изображение будет загружено в ближайшее время)
Чем прямая линия отличается от кривой?
Прямая линия
Кривая линия
Кривые линии различных типов
Кривые линии можно разделить на несколько категорий. Вот они:
Простая кривая — это кривая, не пересекающая сама себя. Мы знаем, что открытая кривая имеет два конца, а замкнутая — нет. Замкнутая кривая — это путь, который может начинаться в любой точке и заканчиваться в одном и том же месте. В результате базовая кривая может быть как открытой, так и замкнутой.
(Изображение будет загружено в ближайшее время)
Непростая кривая — это кривая, которая пересекается сама с собой при изменении направления.
Непростые кривые могут быть открытыми или замкнутыми, как и простые кривые.
Алгебраическая кривая — это плоская кривая с набором точек на евклидовой плоскости, которые выражаются в терминах многочленов. Степень полинома обозначает степень кривой.
C = {(a, b) ∈ R2: P(a, b) = 0}
Эта кривая не совпадает с алгебраической кривой. Трансцендентная кривая определяется как кривая, которая не представляет алгебраическую форму. Наряду с прямой линией эта кривая может иметь множество точек пересечения. В результате многочлен, основанный на a и b, не является трансцендентной кривой.
Линия (кривая) — Математическая энциклопедия
Геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется по-разному в разных разделах геометрии.
В элементарной геометрии понятие кривой четко не определено и иногда определяется как «длина без ширины» или как «граница поверхности».
В элементарной геометрии изучение кривой по существу сводится к рассмотрению примеров (прямая, отрезок, многоугольник, окружность и т. д.). Не располагая общими методами, элементарная геометрия достаточно глубоко ушла в изучение свойств конкретных кривых (конических сечений, некоторых алгебраических кривых высших порядков и трансцендентных кривых), применяя в каждом случае специальные методы.
В аналитической геометрии кривая на плоскости определяется как набор точек, координаты которых удовлетворяют уравнению $ F ( x , y ) = 0 $. На функцию $F$ необходимо наложить ограничения так, чтобы, с одной стороны, уравнение имело бесконечное множество решений, а с другой стороны, чтобы это множество решений не заполнило «кусок плоскости».
Важный класс кривых составляют кривые, для которых функция $F(x,y)$
является многочленом от двух переменных; в этом случае кривая, определяемая уравнением $F(x,y) = 0$
называется алгебраическим. Алгебраические кривые, заданные уравнением первой степени, являются прямыми линиями.
Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или кривую, которая распадается на две прямые (которые могут совпадать). В алгебраической геометрии рассматриваются алгебраические кривые, заданные уравнениями высших степеней. Их теория приобретает большую стройность, если рассмотрение ведется в комплексной проективной плоскости. В этом случае алгебраическая кривая задается уравнением вида
9{3}) = 0,
$$
где $F$ — однородный многочлен от трех переменных — проективных координат точек.
Для тех разделов математики, в которых преобладают методы теории функций (анализ, дифференциальная геометрия и др.), естественным определением кривой является ее задание параметрическими уравнениями. Таким образом, в случае плоскости кривая, заданная параметрическими уравнениями
$$ \тег{1} х = \ фи ( т) , \ \ у = \psi ( т) , $$
где $\phi(t)$
и $ \psi ( t) $
— непрерывные функции на отрезке $ a \leq t \leq b $,
— множество точек $(x,y)$
соответствующие всем возможным значениям параметра $t$
при условии, что эти точки рассматриваются в определенном порядке: Если точка $ M _ {1} $
соответствует значению $ t _ {1} $
и $ М _ {2} $
до $t_{2}$,
затем $ M _ {1} $
считается предшествующим $ M _ {2} $
если $ t _ {1} < t _ {2} $;
точки, соответствующие различным значениям параметра, считаются различными.
Уравнения $ x = \phi _ {1} ( t _ {1} ) $,
$ y = \psi _ {1} ( t _ {1} ) $,
$ t _ {1} \in [ a _ {1} , b _ {1} ] $,
задайте ту же кривую, что и уравнения (1), если существует гомеоморфизм $ \lambda ( t _ {1} ) = t $
интервала $ [ a _ {1} , b _ {1} ] $
на интервал $[a,b]$,
$ \lambda ( _ {1} ) = а $,
$ \ лямбда ( b _ {1} ) = b $,
такой, что $ \phi ( \lambda ( t _ {1} ) ) = \phi _ {1} ( t _ {1} ) $
и $ \ psi ( \ lambda ( t _ {1} ) ) = \ psi _ {1} ( t _ {1} ) $.
Аналогично кривая в произвольном топологическом пространстве $X$
определяется параметрическим уравнением вида $x = \phi(t)$,
где $\фи$
является функцией вещественной переменной $t$,
непрерывна на $[a,b]$,
значениями которых являются точки $x$
$Х$.
Наряду с этим подходом существует и другая точка зрения (К. Джордан, 1882 г.) на определение кривой параметрическими уравнениями: Кривая – это множество точек плоскости, координаты которых являются непрерывными функциями $ x = \phi (т)$,
$ у = \psi ( т) $
параметра $ t $
указан на интервале $[a,b]$;
теперь точки, соответствующие различным значениям параметра, но имеющие одинаковые координаты, не считаются различными, а множество, составляющее кривую, не считается упорядоченным по значениям $t$.
Это определение можно обобщить на любое топологическое пространство: множество точек топологического пространства, являющееся непрерывным образом интервала, называется кривой в смысле Жордана.
Однако непрерывные функции $ \phi ( t) $ и $\psi(t)$, $ 0 \leq t \leq 1 $, построены так, что множество точек, координаты которых определяются этими функциями, заполняют квадрат $ 0 \leq x , y \leq 1 $( см. кривую Пеано). В более общем смысле любой локально связный континуум (т. е. континуум, каждая точка которого имеет произвольную малую связную окрестность) является непрерывным образом интервала (теорема Мазуркевича). Таким образом, не только квадрат, но и куб произвольной размерности и даже бесконечномерный гильбертов куб являются непрерывными образами интервала.
Вышеизложенное показывает, что кривую нельзя определить как непрерывный образ интервала, если не накладывать дополнительных ограничений на отображение. Так, в ДГ эти ограничения задаются наложением условий существования производных различных порядков функций, входящих в параметрическое определение кривой.
С другой стороны, существуют континуумы, которые естественно рассматривать как кривые, но которые, не будучи локально связными, не являются непрерывными образами интервала. Таков, например, континуум, определяемый условиями: $y = \sin(1/x)$,
$ 0 < х \leq 1 $;
$х=0$,
$ - 1 \leq y \leq 1 $(
Рис. а).
Рисунок: l059020a
Более общее определение кривой для случая плоскости было дано Г. Кантором в 70-х гг. 19 в. в связи с созданием теории точечных множеств. Плоский континуум, в любой окрестности каждой его точки есть точки плоскости, не принадлежащие континууму, называется кривой Кантора. Важным примером кривой Кантора является ковер Серпинского, построенный следующим образом. Квадрат $Q$
стороны 1 делится на девять равных квадратов прямыми, параллельными его сторонам, и удаляются все внутренние точки центрального квадрата (рис. б, $ n = 1 $).
То же самое проделывается с каждым из оставшихся восьми квадратов первого ранга, и получается 64 квадрата второго ранга (рис.
{n}$.
Пересечение полученных таким образом множеств и есть ковер Серпинского (рис. б).
9\простой $
гомеоморфна $L$.
Ковер Серпинского представляет собой локально связный континуум и, следовательно, является непрерывным образом интервала.
В топологии используется понятие кривой, введенное в 1921 г. П.С. Урысона, что является более общим (но не слишком). Определение кривой формулируется следующим образом: Кривая — это одномерный континуум, т. е. связное компактное метрическое пространство $C$
каждая точка которого имеет сколь угодно малую окрестность с границей нулевой размерности. Другими словами, для любого $ \epsilon > 0 $
пространство $C$
можно представить в виде суммы конечного числа замкнутых множеств диаметра меньше $ \epsilon $
обладающее тем свойством, что никакие три из этих множеств не имеют общей точки. Ковер Серпинского удовлетворяет этому определению кривой, поэтому любая кривая Кантора также является кривой в смысле Урысона. Наоборот, если плоский континуум является кривой в смысле Урысона, то это кривая Кантора.
\prime $
$ млн $
гомеоморфна $C$,
строится следующим образом. Куб $K$
ребер 1 разделен плоскостями, параллельными его граням, на 27 равных кубов. От $К$
удаляется центральный куб и все кубы этого подразделения, смежные с ним по двумерным граням. Получается множество $ K _ {1} $
состоящая из оставшихся 20 замкнутых кубиков первого ранга. Поступая точно так же с каждым кубом первого ранга, получаем множество $ K _ {2} $
состоящая из 400 кубиков второго ранга (рис. г). Продолжая этот процесс до бесконечности, получим последовательность континуумов $ K _ {1} \supset K _ {2} \supset \dots $
пересечение которых представляет собой одномерный континуум $M$,
называется универсальной кривой Менгера.
9\простой $
имеет мощность не менее $\mathfrak m$.
Точки кривой классифицируются по индексу их ветвления следующим образом.
1) Точки с индексом ветвления $n$, где $n$ является натуральным числом.
2) Точки неограниченного индекса ветвления $\omega$.
(точка $ x $
кривой $ C $
имеет индекс ветвления $ \omega $
если для любого числа $ \epsilon > 0 $
существует открытое множество, содержащее $x$,
диаметром менее $ \epsilon $
и граница которого состоит из конечного множества точек, и если для любого натурального числа $ n $
есть число $ \epsilon _ {n} > 0 $
такое, что граница любого открытого множества, содержащего $ x $
и диаметром менее $ \epsilon _ {n} $
состоит не менее чем из $n$
точки.
{n}}\dots$
имеет неограниченно возрастающий индекс ветвления $ \omega $
в $О$(
Рис. д).
9{n} } \точки $
имеет счетный индекс ветвления $ \aleph _ {0} $
в каждой точке $ O a _ {0} $(
Рис. е). е) Кривая, состоящая из отрезков, соединяющих $O$
всем точкам канторовского множества, лежащим на интервале $ 0 \leq x \leq 1 $,
$у = 0$,
имеет континуальный индекс ветвления $ \mathfrak c $
в каждой его точке (рис. ж).
Рисунок: l059020g
ж) Ковер Серпинского также имеет континуальный индекс ветвления в каждой своей точке.
Если кривая вообще не имеет точек ветвления, т. е. если в каждой точке кривой показатель ветвления равен 1 или 2, то эта кривая является либо простой дугой (топологическим образом отрезка), либо простая замкнутая кривая (топологический образ окружности). Если индекс ветвления кривой во всех точках равен двум, то это простая замкнутая кривая, а если кривая, не имеющая точек ветвления, имеет конечные точки (оказывается, что их неизменно две), то это простая дуга.
Если кривая имеет только конечное число точек ветвления и индекс ветвления каждой из них также конечен, то такую кривую можно разбить на конечное число простых дуг, не имеющих общих точек, кроме концов.
Окружность — это единственная кривая, все точки которой имеют одинаковый конечный индекс ветвления 2; не существует других кривых, имеющих во всех точках один и тот же конечный индекс ветвления, и если все точки кривой $L$ иметь индекс ветвления больше или равный $n$, то есть точка на $L$ с индексом ветвления больше или равным 2$ n — 2$; для любого натурального числа $n$ существует кривая, состоящая только из точек, имеющих индекс ветвления $ n $ и $2n-2$( теорема Урысона). Пример кривой, состоящей только из точек с индексом ветвления 3 или 4, строится следующим образом.
Рисунок: l059020h
В равностороннем треугольнике со стороной 1 проводят три линии, соединяющие середины, и удаляют от них внутренние точки образованного ими треугольника. С каждым из оставшихся трех треугольников первого ранга проводится аналогичная операция, в результате которой получается девять треугольников второго ранга.
Действуя таким же образом с ними, получается 27 треугольников третьего ранга и т. д. для каждого натурального числа $ n $.
Пересечение множеств, полученных в результате этих операций, представляет собой кривую $C$(
Рис. з). Кривая, состоящая из точек с индексом ветвления 3 или 4, состоит из двух континуумов $ C _ {1} $
и $C_{2}$,
каждый из которых гомеоморфен $C$
и которые не имеют общих точек, кроме тех, которые соответствуют вершинам основного треугольника континуума $C$.
Существуют также кривые, которые имеют неограниченный индекс ветвления, счетный индекс ветвления и континуальный индекс ветвления во всех точках.
Каталожные номера
| [1] | P.S. Александров, «Einführung in die Mengenlehre und die Theorie der reellen Funktionen», Deutsch. Verlag Wissenschaft. (1956) (Перевод с русского) MR0168706 |
| [2] | К. Куратовский, «Топология», 2 , акад. Пресса (1968) (Translated from French) MR0259835 Zbl 0849.01044 Zbl 0528.54033 Zbl 1081.54501 Zbl 0383.54001 Zbl 0323.54010 Zbl 0274.54007 Zbl 0267.54002 Zbl 0247.54001 Zbl 0163.17002 Zbl 0158.40901 Zbl 0158.40802 Zbl 0148.42801 Zbl 0104.27402 Zbl 0098.24110 Zbl 0137.15604 Zbl 0041.09604 Zbl 0041.09603 Zbl 0008.13202 Zbl 56.0517.04 |
| [3] | К. Менгер, «Курвентеория», Тойбнер (1932) MR0221475 MR1549694 Zbl 0005.41504 Zbl 58.1205.02 |
| [2] 260 А.С. Пархоменко, «Что такое кривая?» , Москва (1954) (на русском языке) | |
| [5] | П.С. Урысон, «Работы по топологии и другим областям математики», 2 , Москва-Ленинград (1951) (на русском языке) |
| [6] | Ф. Хаусдорф, «Grundzüge der Mengenlehre», Лейпциг (1914) (Перепечатанный (неполный) английский перевод: Теория множеств, Челси (1978))0068 |
Комментарии
«Кривая по Жордану» (т.
е. непрерывный образ единичного интервала $I$)
также называется континуумом Пеано. Его не следует путать с понятием жордановой кривой (пространство, гомеоморфное окружности, также называемое простой замкнутой кривой).
Упомянутая выше теорема Мазуркевича широко известна как теорема Хана–Мазуркевича [a1], 6.3.14.
Ковер Серпинского также называют универсальной кривой Серпинского.
Кривая на рис. h была построена В. Серпинским [a3].
Список литературы
| [A1] | R. Engelking, «Общая топология», Heldermann (1989) MR1039321 ZBL 0684.54001 |
| [A2] | 6. Р. Р. Р. Р. Р., R., R., R., R., R., Demel,6. и PWN (1978), стр. 19; 50 MR0482696 MR0482697 Zbl 0401.54029|
| [a3] | В. Серпинский, «Sur un courbe dont tout point est un point de ветвления» CR Hebdomaires Acad. науч. Paris , 160 (1915) pp. |
Добавить комментарий