Как называется кривая линейка: «Кривая» линейка, 6 букв, сканворд
«Кривая» линейка, 6 букв, сканворд
Подошло Не подошло
«Кривая» линейка
Альтернативные описания
• инструмент портного и чертежника
• инструмент, который применяют при черчении, когда циркуль не помогает
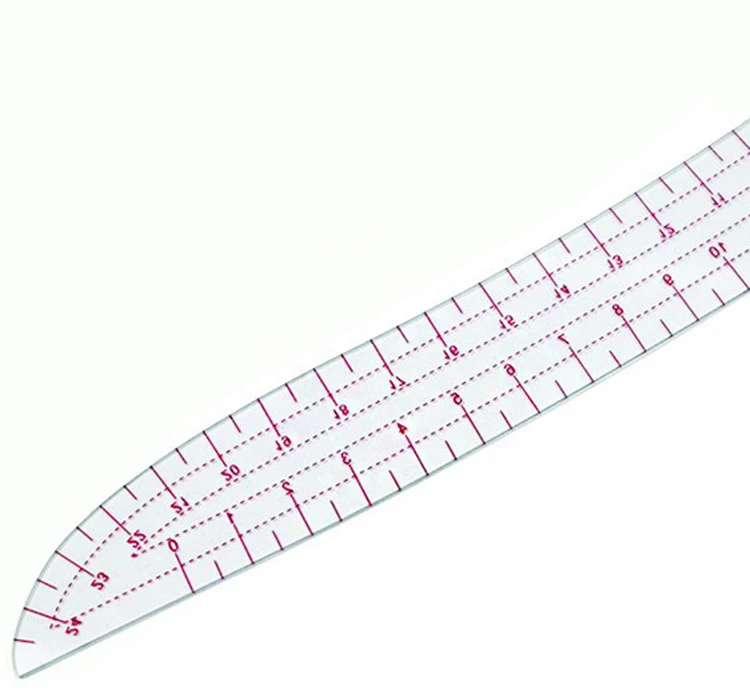
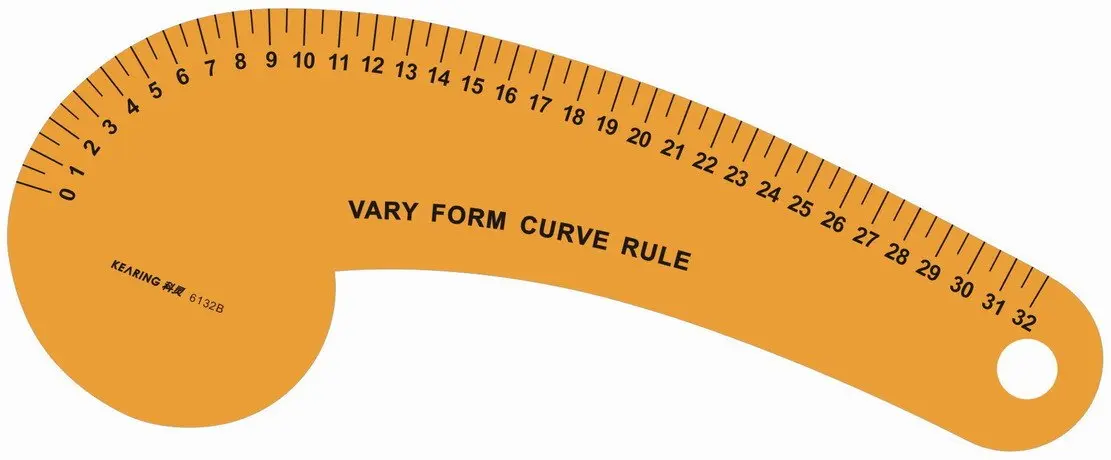
• фигурная линейка для вычерчивания кривых линий
• чертежный инструмент для вычерчивания кривых линий
• чертежный инструмент, фигурная линейка
• шаблон, модель, применяемые при изготовлении изделий сложного профиля
• фигурная линейка
• «криволинейка»
• какую линейку можно получить, если у известного шоумена поменять первую букву?
• линейка для того, кто предпочитает окольные пути
• фигуристая линейка
• линейка закройщика
• инструмент для разметки
• линейка-кривляка
• шаблон для обводки
• шаблон, линейка
• изогнутая линейка
• «кривая» линейка
• линейка модельера
• шаблон для обводов
• кривая линейка портного
• линейка с загогулинами
• инструмент для разведки
• линейка для выкроек одежды
• чертежный инструмент
• «кривляка» среди линеек
• чертежная линейка
• линейка с изгибами
• загогулистая линейка
• линейка с выкрутасами
• линейка
• линейка-шаблон с выкрутасами
• линейка «ищущих окольные пути»
• фигурный шаблон
• «портнографическая» линейка
• швейная «линейка»
• рифма к Цекало
• кривой трафарет чертежника
• «вертлявая» линейка закройщика
• линейкакривляка
• криволинейный шаблон портного
• фигурная линейка портного
• линейка для кривых линий
• линейка «любителя окольных путей»
• шаблон
• неровная линейка
• хитроумная линейка
• «букет кривых»
• линейка обтекаемых форм
• шаблонная линейка
• Инструмент для вычерчивания кривых линий
• Чертежный инструмент для проведения или проверки кривых линий
• Измерительный инструмент, шаблон
• Фигуристая линейка
• «Букет кривых»
• «Вертлявая» линейка закройщика
• «Кривляка» среди линеек
• «Криволинейка»
• «Линейка» закройщика
• «Портнографическая» линейка
• какую линейку можно получить, если у известного шоумена поменять первую букву
• линейка «ищущих окольные пути»
• линейка «любителя окольных путей»
• линейка-шаблон
• ср. выкройка, образец для внешних очерков вещи; кривые правила разного вида, для криволинейных чертежей, особенно корабельных; вытесанный из досок по чертежу, в полную величину, образец, для обделки по нем корабельных членов и железных скреплений; вырезка по чертежу в дощечке, для обделки литейных болванов, для тяги штукатурных карнизов; снаряд для калиброванья, измеренья ядер. Пск. твер. бот или ботало, двухсаженная мутовка рыбаков, для сгону рыбы; вероятно от лакать, пугать; арх. деревянные путы на оленя, колодка на ногу; вероятно, от лекан м. перм. отрубок, чурбашек. Лекальный, к лекалу относящ. Лекальщик м. обделывающий лекала. Лекальная ж. мастерская, где изготовляют и пригоняют лекала по чертежам. Лекать пск. твер. вернее лякать малорос. пугать, загонять рыбу лекалом, рыбачить при помощи его, ботать
выкройка, образец для внешних очерков вещи; кривые правила разного вида, для криволинейных чертежей, особенно корабельных; вытесанный из досок по чертежу, в полную величину, образец, для обделки по нем корабельных членов и железных скреплений; вырезка по чертежу в дощечке, для обделки литейных болванов, для тяги штукатурных карнизов; снаряд для калиброванья, измеренья ядер. Пск. твер. бот или ботало, двухсаженная мутовка рыбаков, для сгону рыбы; вероятно от лакать, пугать; арх. деревянные путы на оленя, колодка на ногу; вероятно, от лекан м. перм. отрубок, чурбашек. Лекальный, к лекалу относящ. Лекальщик м. обделывающий лекала. Лекальная ж. мастерская, где изготовляют и пригоняют лекала по чертежам. Лекать пск. твер. вернее лякать малорос. пугать, загонять рыбу лекалом, рыбачить при помощи его, ботать
• швейная «линейка»
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое изогнутая линия? Определение, типы, примеры, факты
Что такое изогнутая линия?
Изогнутая линия, как следует из названия, представляет собой изогнутую линию. Мы видим вокруг себя изогнутые объекты. Изогнутые линии также известны как изогнутые линии. Обратите внимание, что линия строго прямая. Кривую можно рассматривать как обобщение линии.
Вы можете заметить, что буквы A, I, T и т. д. не имеют изогнутых линий. Однако мы не можем писать такие буквы, как B, C, D и т. д., без изогнутой линии. В каких еще повседневных наблюдениях вы видите изогнутые линии? Усы, кривая линия над рядом нот в нотах, радуга, кривая дорога, кудрявые волосы!
Связанные игры
Изогнутая линия: определение
Изогнутая линия — это тип линии, которая не является прямой и изогнутой. Он непрерывный и плавный, без резких поворотов.
Он непрерывный и плавный, без резких поворотов.
Мы знаем, что кривизна прямой равна нулю. Следовательно, когда кривизна линии не равна нулю, мы называем ее криволинейной линией.
Представьте, что жуку нужно переместиться из точки А в точку Б. Какими способами жук может добраться из точки А в точку Б?
Жук может добраться из пункта А в пункт Б несколькими путями. На приведенных рисунках показаны некоторые пути, по которым муравей может добраться из пункта А в пункт Б.
Мы видим, что на первых четырех рисунках муравей менял свое направление при путешествии из точки А в точку Б, то есть он не следовал одному постоянному направлению. Однако на последнем рисунке муравей двигался прямо, и расстояние, которое он прошел, было самым коротким. Движение от одной точки к другой порождает прямые или кривые линии.
Связанные рабочие листы
Примеры изогнутой линии
Приведенные выше буквы и цифры состоят только из кривых.
Прямые линии и изогнутые линии
Давайте посмотрим на разницу между изогнутыми и прямыми линиями.
Чем прямая линия отличается от кривой?
Некоторые факторы, такие как кривизна, случайный изгиб и направление, делают прямую линию отличной от кривой. Все эти различные типы кривых на графике также упоминаются.
Различные типы кривых линий
Давайте обсудим некоторые типы кривых, образованных кривыми линиями.
Открытая криваяНезамкнутая кривая не заключает в себе никакой области и имеет две конечные точки. Примеры незамкнутых кривых:
Замкнутая криваяЗамкнутая кривая не имеет конечных точек и охватывает площадь (или область). Он образуется путем соединения концов открытой кривой вместе. Окружности и эллипсы формируются из замкнутых кривых. Окружность — это замкнутая кривая, образованная при движении точки по плоскости так, что она находится на постоянном расстоянии от своего центра.
Примеры замкнутых кривых:
Простая кривая Простая кривая определяется как кривая, которая не пересекает и не пересекает саму себя. Простая кривая меняет направление, но не пересекает себя при изменении направления. Он может быть открытым и закрытым.
Простая кривая меняет направление, но не пересекает себя при изменении направления. Он может быть открытым и закрытым.
Кривая, пересекающая собственную траекторию, называется сложной кривой.
Забавные факты о изогнутых линиях
- Геометрия — это раздел математики, изучающий различные фигуры и тела, состоящие из прямых и изогнутых линий. 9{n} + \text{bx} + c; а \neq 0$
Заключение
В этой статье мы узнали о изогнутых линиях, широко известных как кривые. Мы видели разные типы кривых. Давайте решим несколько задач для лучшего понимания.
Решенные примеры на изогнутых линиях
1. Определите незамкнутые и замкнутые кривые на рисунке ниже.
Решение:
Как мы видим, открытые кривые — это (b), (d) и (f).
Замкнутые кривые — это те, у которых конечные точки соединены вместе, (a), © и (e).
2. Какие из следующих букв обозначают открытые кривые?
O, U, C, D, S
Альтернативные теги: изогнутые линии в алфавитах
Решение:
Буквы, обозначающие две открытые кривые, U, C и S. конечные точки. Однако буквы O и D являются замкнутыми кривыми.
конечные точки. Однако буквы O и D являются замкнутыми кривыми.
3. Определите простые и сложные кривые.
8, в, и, в, о
Альтернативные теги: изогнутые линии
Решение:
Простые кривые: кривые, которые не пересекаются при изменении направления. т. е., c, o
Непростые кривые: кривые, которые пересекают свою траекторию, т. е. 8, Q, &
4. Определите тип кривой на данном рисунке.
Решение:
Кривая на данном рисунке является открытой кривой.
Практические задачи
1
Буква O является примером _______ .
Непростая замкнутая кривая
Простая незамкнутая кривая
Простая замкнутая кривая
Непростая кривая
Правильный ответ: Простая замкнутая кривая
Это простая замкнутая кривая, потому что она не пересекает сама себя и ее концы сходятся заключить пространство.
2
Определите тип кривой на данном рисунке:
Открытая кривая
Простая незамкнутая кривая
Простая кривая
Непростая кривая
Правильный ответ: Непростая кривая
Кривая на данном рисунке не является простой кривой, так как она пересекает свою собственную траекторию.
3
Какая из следующих кривых является незамкнутой?
Парабола
Окружность
Эллипс
Ничего из вышеперечисленного
Правильный ответ: Парабола
Окружность и эллипс являются замкнутыми кривыми. Парабола, однако, является открытой кривой.
4
Определите тип кривой на данном рисунке:
Изокванта
Трансцендентальная кривая
Простая кривая
Непростая кривая
Правильный ответ: Непростая кривая
Кривая на данном рисунке — непростая кривая.
5
Определите тип кривой на данном рисунке:
Замкнутая
Простая кривая
Открытая кривая
Ничего из вышеперечисленного
Правильный ответ: Открытая кривая
Кривая на данном рисунке является открытой изгиб.
Часто задаваемые вопросы
Определение прямой линии.
Прямая линия может быть определена как линия, очерченная точкой, движущейся в постоянном направлении.
Что такое кривизна линии?
Кривизна показывает, насколько быстро кривая меняет направление в данной точке.
Какая польза от изогнутых линий?
Изогнутые линии обычно используются для графического представления различных типов функций.
Какие буквы английского алфавита изогнуты?
Несколько изогнутых букв английского алфавита: C, S, O и т. д.
Как называется самая высокая или самая низкая часть кривой?
Точка, в которой кривая находится на самом высоком или самом низком уровне, называется вершиной.
Изогнутые линии – значение, примеры, типы и часто задаваемые вопросы
Изогнутая линия определяется как линия, которая не прямая, а изогнутая. В идеале прямая линия имеет нулевую кривизну, тогда как изогнутая линия имеет ненулевую кривизну и является непрерывной и гладкой. Кривые — это выдающиеся фигуры, встречающиеся повсюду вокруг нас. Вы можете заметить изгибы в искусстве, украшении или вообще предмете, а кривые — это фигуры, которые можно увидеть повсюду вокруг вас. Первоначально линии могли быть изогнутыми или прямыми. В сегодняшнем математическом использовании, для точного различия, кривая — это что-то изогнутое, а линия — это что-то прямое.
В идеале прямая линия имеет нулевую кривизну, тогда как изогнутая линия имеет ненулевую кривизну и является непрерывной и гладкой. Кривые — это выдающиеся фигуры, встречающиеся повсюду вокруг нас. Вы можете заметить изгибы в искусстве, украшении или вообще предмете, а кривые — это фигуры, которые можно увидеть повсюду вокруг вас. Первоначально линии могли быть изогнутыми или прямыми. В сегодняшнем математическом использовании, для точного различия, кривая — это что-то изогнутое, а линия — это что-то прямое.
Кривые линии часто используются для графического представления функций, поскольку это одна из важнейших тем в области математики.
Differentiate Between Curved Lines And Straight Lines
Curved Line | Straight Line |
A smoothly bent line which is not straight is called a Curved Line. | Кратчайшая линия, соединяющая любые две точки, называется прямой линией. |
Точки, определяющие кривую, меняют направление от одной точки к другой. | Прямая линия представляет собой последовательность нескольких точек, выровненных в одном направлении. |
Изогнутая линия всегда имеет ненулевую кривизну, которая может быть положительной или отрицательной. | Прямая линия всегда имеет нулевую кривизну. |
Изогнутые линии не двигаются в одном направлении. Направление постоянно меняется от одной точки к другой. | Прямые линии движутся в одном направлении. |
Примеры изогнутых линий
Существует множество примеров изогнутых линий. Наиболее распространенным и ярким примером изогнутых линий являются буквы алфавита C и S.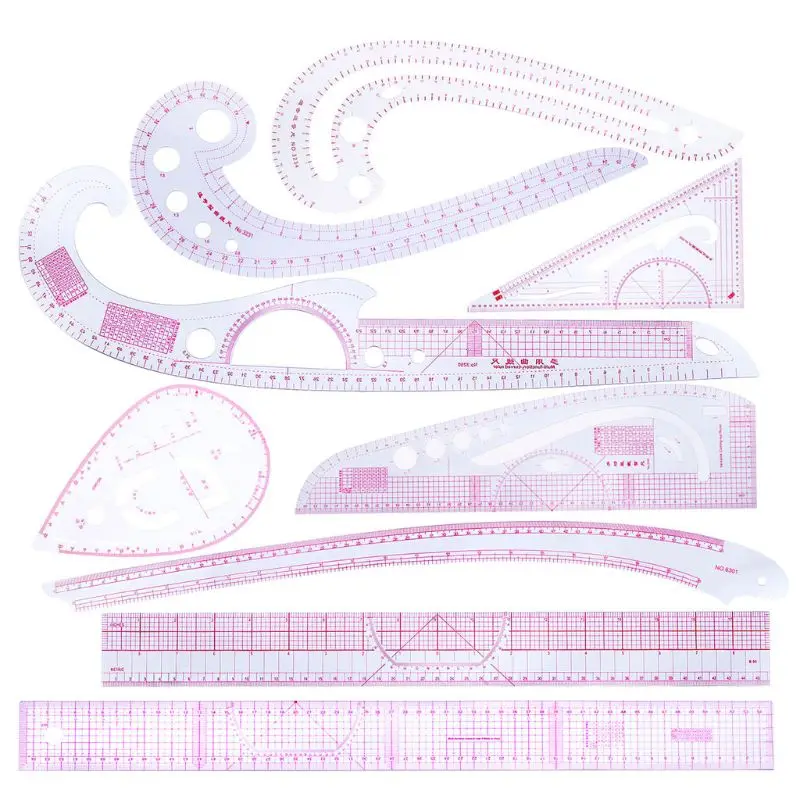 Эти буквы алфавита изогнуты. Напротив, другие буквы, такие как L, N, A, Z и другие, являются подходящими примерами прямых линий, поскольку они не являются кривыми, а являются соединенными сегментами двух или более последовательных линий.
Эти буквы алфавита изогнуты. Напротив, другие буквы, такие как L, N, A, Z и другие, являются подходящими примерами прямых линий, поскольку они не являются кривыми, а являются соединенными сегментами двух или более последовательных линий.
Типы изогнутых линий
Существует множество различных типов изогнутых линий. Тем не менее, есть несколько известных типов изогнутых линий:
1. Открытая кривая
Кривая или кривая называется открытой, если ее конечные точки не пересекаются. В открытой изогнутой линии конечные точки никогда не встречаются.
Парабола — прекрасный пример незамкнутой кривой.
2. Замкнутая кривая
Кривая называется замкнутой, если ее начальная точка совпадает с конечной точкой.
Круг или затмение — прекрасный пример замкнутой кривой.
3. Простая кривая
Простая кривая
Простая кривая не пересекает сама себя. Некоторые кривые самопересекающиеся; однако простая кривая не пересекается сама с собой.
4. Алгебраическая кривая
Алгебраическая кривая — это плоская кривая, в которой множество точек размещено на евклидовой плоскости и представлено в виде многочленов. Степень кривой обозначается степенью многочлена.
Например, C = {(a, b) ∈ R2: P(a, b) = 0}
5. Трансцендентальная кривая
изгиб. Трансцендентная кривая состоит из бесконечного числа точек перегиба и множества точек пересечения, которые будут прямыми. Это не многочлен в точках a и b.
6. Кривая изокванты
Термин «изокванта» представляет собой объединение двух терминов: «изо» означает «равно», а слово «количество» относится к количеству. Таким образом, термин изокванта определяется как кривая выпуклой формы, образованная соединением точек. Кривая изокванты помогает организациям и предприятиям регулировать затраты, чтобы максимизировать производство и прибыль.
Кривая изокванты помогает организациям и предприятиям регулировать затраты, чтобы максимизировать производство и прибыль.
Изогнутая линия
«Изогнутая линия» или просто «Кривая» — это непрямая линия. Кривые можно найти повсюду вокруг нас. Кривые можно найти повсюду вокруг нас, будь то искусство, декор или повседневная жизнь. В этом посте мы изучим концепцию изогнутой линии, а также различные типы изогнутых линий и несколько экземпляров.
Что такое кривая линия?
Изогнутая линия — это изогнутая, а не прямая линия. В идеальной ситуации он должен быть плавным и непрерывным. Другими словами, кривая — это набор точек, которые напоминают прямую линию и попадают между двумя точками. Кривизна прямой линии, как известно, равна нулю. В результате мы можем назвать линию изогнутой, если ее кривизна больше нуля. Различные виды изогнутых линий изображены на диаграмме ниже.
(Изображение будет загружено в ближайшее время)
Чем прямая линия отличается от кривой?
Прямая линия
Кривая линия
Кривые линии различных типов
Кривые линии можно разделить на несколько категорий. Вот они:
Вот они:
Простая кривая — это кривая, не пересекающая сама себя. Мы знаем, что открытая кривая имеет два конца, а замкнутая — нет. Замкнутая кривая — это путь, который может начинаться в любой точке и заканчиваться в одном и том же месте. В результате базовая кривая может быть как открытой, так и замкнутой.
(Изображение будет загружено в ближайшее время)
Непростая кривая — это кривая, которая пересекается сама с собой при изменении направления. Непростые кривые могут быть открытыми или замкнутыми, как и простые кривые.
Алгебраическая кривая — это плоская кривая с набором точек на евклидовой плоскости, которые выражены в терминах многочленов. Степень полинома обозначает степень кривой.
C = {(a, b) ∈ R2: P(a, b) = 0}
Эта кривая не совпадает с алгебраической кривой. Трансцендентная кривая определяется как кривая, которая не представляет алгебраическую форму. Наряду с прямой линией эта кривая может иметь множество точек пересечения.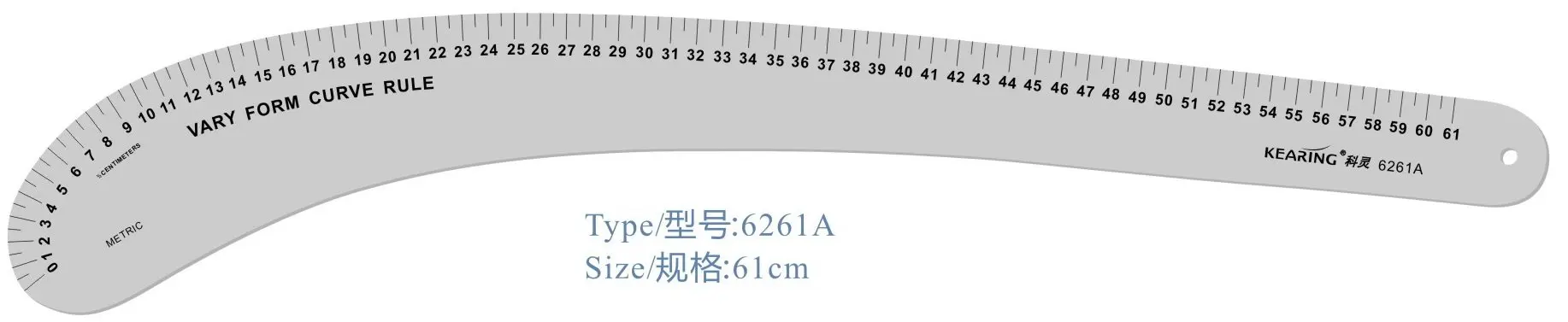

 Кривая линейка Яндекс.Карт
Кривая линейка Яндекс.Карт
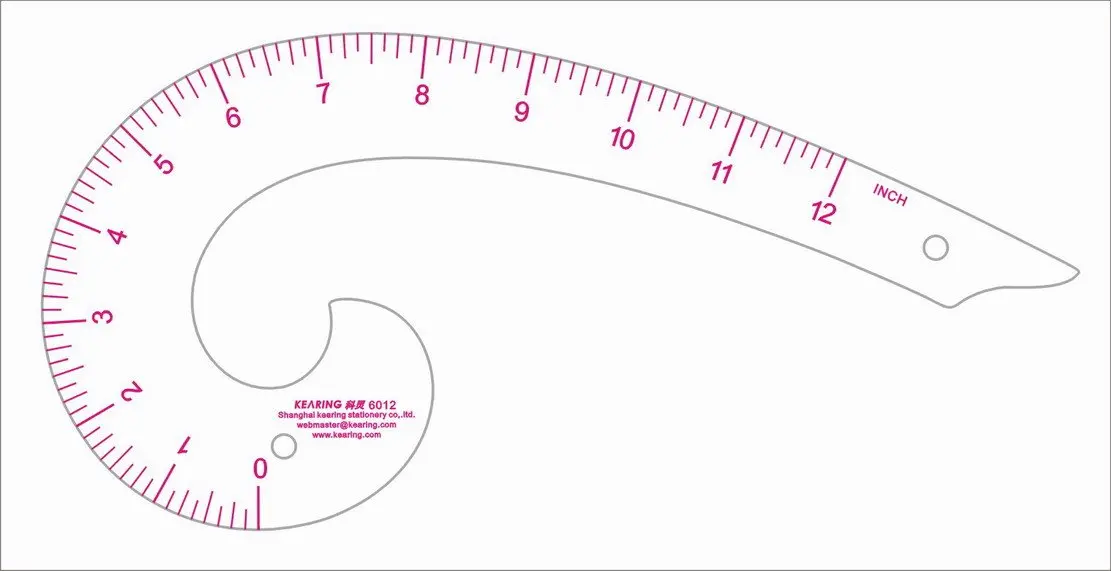
 Это экватор.
Это экватор.
 Кривая линейка Яндекс.Кар
Кривая линейка Яндекс.Кар
 Блин. Затупил немного — нет, все локсодромии прямые только на Меркаторе. Всё. То есть должны быть и цилиндричность, и равноугольность. Wiki it!
Блин. Затупил немного — нет, все локсодромии прямые только на Меркаторе. Всё. То есть должны быть и цилиндричность, и равноугольность. Wiki it!
 Просто глобус, который можно приближать-удалять. Там, я так понимаю, вообще искажений нет. Это ж глобус.
Просто глобус, который можно приближать-удалять. Там, я так понимаю, вообще искажений нет. Это ж глобус. 48184250%2C5.20218746~130.07797405%2C23.02019655
48184250%2C5.20218746~130.07797405%2C23.02019655 (В смысле точек бесконечно много поставить)
(В смысле точек бесконечно много поставить)
Добавить комментарий